PHPSimplex

Otimizar os recursos com Programação Linear

Tweetar

Exemplo (parte 2): método Gráfico

Solução através do método gráfico o seguinte problema:

Maximizar	Z = f(x,y) = 3x + 2y
sujeita às restrições:	2x + y ≤ 18
	2x + 3y ≤ 42
	3x + y ≤ 24
	x ≥ 0 , y ≥ 0

1. Inicialmente, o sistema de coordenadas da associação de um eixo com variável "X" e o outro o "Y" é desenhado (geralmente associa-se "x" em relação ao eixo horizontal e o "y" ao vertical), como pode ser visto na figura.
2. Nestes eixos, marca-se uma escala numérica apropriada aos valores que podem assumir as variáveis conforme as restrições do problema. Para isto, em cada restrição anulam-se todas as variáveis, exceto aquelas que correspondem a um eixo concreto, estabelecendo o valor adequado para este eixo. Este processo é repetido para cada um dos eixos.
3. As restrições são representadas a seguir. Primeiramente, desenha-se a reta que é obtida ao considerar a restrição como uma igualdade. Ela é representada como o segmento que une A com B e região que delimita esta restrição é indicada pela cor AMARELA. O processo é repetido com as outras restrições, ficando delimitada a região de cor AZUL e VERMELHO para a segunda e terceira restrição respectivamente.
4. A região viável é a interseção das regiões definidas tanto pelo conjunto de restrições, como pelas condições de não negatividade das variáveis, ou seja, ambos os eixos de coordenadas. Tal região viável é representada pelo polígono O-F-H-G-C, de cor VIOLETA.
   
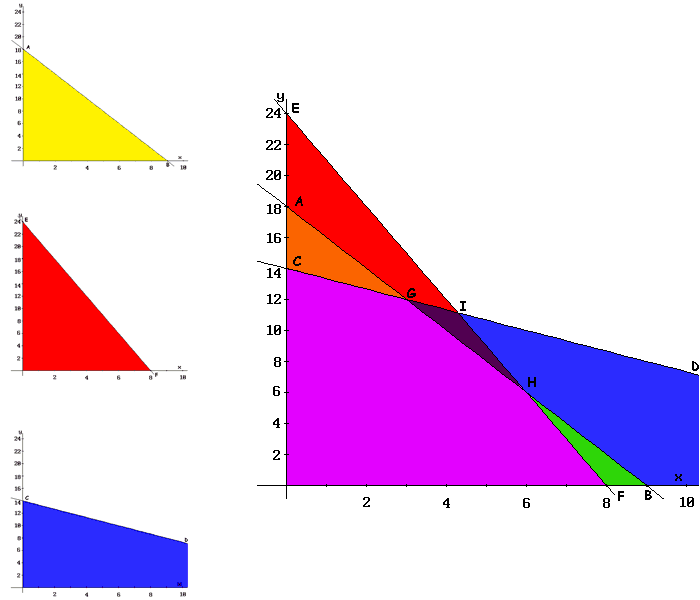
5. Como existe uma região viável, passamos a determinar os seus pontos extremos, ou vértices do polígono que representa. Esses vértices são os pontos candidatos a soluções ótimas. Neste exemplo são os pontos O-F-H-G-C da figura.
6. Finalmente, a função objetivo (3x + 2y) em cada um destes pontos (resultado determinado na tabela abaixo) é avaliada. Como o ponto G fornece o maior valor para a função Z e o objetivo é maximizar, este ponto é a solução ideal: Z = 33 con x = 3 e y = 12.

Ponto extremo	Coordenadas (x,y)	Valor objetivo (Z)
O	(0,0)	0
C	(0,14)	28
G	(3,12)	33
H	(6,6)	30
F	(8,0)	24

Comparação do método Gráfico com o método Simplex

As tabelas construídas, sucessivamente, durante o método Simplex vão fornecendo o valor da função objetivo em diferentes vértices da região viável, ao mesmo tempo, ajustando os coeficientes das variáveis iniciais e de folga.

Na tabela inicial foi calculado o valor da função objetivo no vértice O, cujas coordenadas (0,0) se correspondem com o valor que têm as variáveis básicas e o resultado é 0.

Tabela I . Iteração 1
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	18	2	1	1	0	0
P4	0	42	2	3	0	1	0
P5	0	24	3	1	0	0	1
Z		0	-3	-2	0	0	0

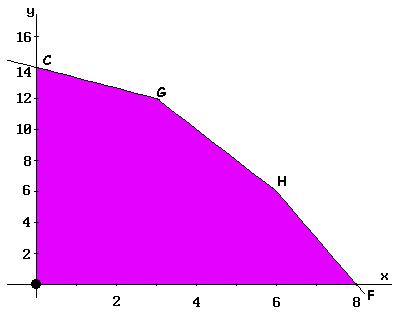
A variável que entra na base do método Simplex determina a que novo vértice será realizado o deslocamento. Neste exemplo, como entra P1 (correspondente ao 'x'), o deslocamento é realizado pela aresta OF até atingir o vértice F, onde é calculado o valor que assume a função Z. Este passo ocorre na segunda iteração do método Simplex, mostrado na Tabela II. Onde foi calculado o valor correspondente à vértice F, obtendo-se um valor Z = 24 para a função.

Tabela II . Iteração 2
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P3	0	2	0	1/3	1	0	-2/3
P4	0	26	0	7/3	0	1	-2/3
P1	3	8	1	1/3	0	0	1/3
Z		24	0	-1	0	0	1

Um novo deslocamento é realizado na aresta FH até chegar em H (dados na tabela III). Na terceira iteração, o valor da função no vértice H é calculado, obtendo-se Z = 30.

Tabela III . Iteração 3
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	6	0	1	3	0	-2
P4	0	12	0	0	-7	1	4
P1	3	6	1	0	-1	0	1
Z		30	0	0	3	0	-1

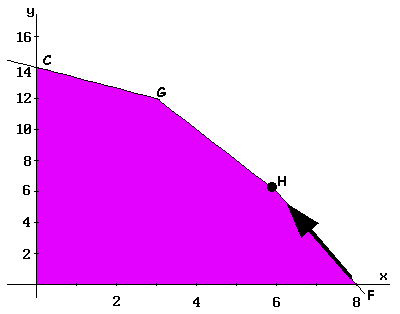
O processo prossegue através da aresta HG, até o vértice G. Os dados obtidos são mostrados na Tabela IV. Neste ponto, o processo termina, e é possível verificar que a solução não é melhorada pela aresta GC até o vértice C (não excede o valor atual da função).

Tabela IV . Iteração 4
			3	2	0	0	0
Base	Cb	P0	P1	P2	P3	P4	P5
P2	2	12	0	1	-1/2	1/2	0
P5	0	3	0	0	-7/4	1/4	1
P1	3	3	1	0	3/4	-1/4	0
Z		33	0	0	5/4	1/4	0

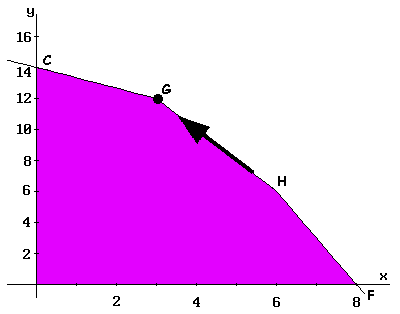
O valor máximo da função objetiva é 33, e corresponde aos valores x = 3 e y = 12 (coordenadas do vértice G).

Com o método gráfico é necessário calcular o valor da função objetivo em cada vértice da região viável, enquanto que o método simplex termina quando o valor ótimo é encontrado.

Resolver com PHPSimplex pelo método Simplex.

Resolver com PHPSimplex pelo método Gráfico.

Copyright ©2006-2024 PHPSimplex. Todos os direitos reservados. Termos e condições.

X