PHPSimplex

Optimiser les ressources avec Optimisation Linéaire

Théorie de la méthode du Simplexe

La méthode du Simplexe est une procédure itérative qui permet d'améliorer la résolution de la fonction objectif à chaque étape. Le processus se termine lorsque vous ne pouvez pas continuer à améliorer la valeur, c'est-à-dire, on a atteint la solution optimale (la valeur la plus élevée ou la plus basse possible, selon le cas).

à partir de la base de la valeur de la fonction objectif en un point quelconque, le procédé est de trouver un autre point qui améliore la valeur précédente. Comme indiqué dans la méthode Graphique, ces points sont les sommets du polygone (ou polyèdre ou polychore, si le nombre de variables est supérieur à deux), qui est la région déterminée par les contraintes que le problème est soumis (dite région faisable). La recherche est effectuée par les déplacements des arêtes du polygone, du sommet courant jusqu'à un élément adjacent qui permet d'améliorer la valeur de la fonction objectif. Chaque fois que la région faisable sera présente, vu que le nombre de sommets et d'arêtes est fini, il est possible de trouver la solution.

La méthode du Simplexe est basé sur la propriété suivante: si la fonction objectif Z ne prend pas sa valeur maximale au niveau du sommet A, puis, il y a une arête dont le point de départ est A et le long de laquelle la valeur de Z augmente.

Il sera nécessaire de tenir compte que la méthode du Simplexe fonctionne uniquement avec les contraintes du problème dont les contraintes sont du type "≤" (inférieur ou égal) et ses coefficients indépendants sont supérieurs ou égaux à 0. Ainsi, les restrictions devraient être normalisées pour répondre à ces exigences avant de commencer l'algorithme du Simplexe. Dans le cas où les contraintes de type "≥" (supérieur ou égal) ou "=" (égal) apparaissent après ce processus, ou on ne peut pas les modifier, il sera nécessaire d'utiliser d'autres méthodes de résolution, étant la méthode de Deux Phases la plus courante.

Adaptation du modèle à la méthode du Simplexe

La forme standard du modèle de problème consiste d'une fonction objectif sous des contraintes déterminées:

Fonction objectif:	c1·x1 + c2·x2 + ... + cn·xn
sous les contraintes:	a11·x1 + a12·x2 + ... + a1n·xn = b1 a21·x1 + a22·x2 + ... + a2n·xn = b2 ... am1·x1 + am2·x2 + ... + amn·xn = bm x1,..., xn ≥ 0

Le modèle doit accomplir les conditions suivantes:

L'objectif sera de maximiser ou minimiser la valeur de la fonction objectif (par exemple, augmenter les bénéfices ou réduire les pertes, respectivement).
Toutes les contraintes doivent être des équations d'égalité (identités mathématiques).
Toutes les variables (Xi) doivent être une valeur positive ou nulle (condition de non-négativité).
Les termes indépendants (bi) de chaque équation doivent être non négatifs.

Nous devons adapter la modélisation du problème à la forme standard pour l'application de l'algorithme du Simplexe.

Type d'optimisation.

Comme mentionné précédemment, l'objectif de la méthode sera d'optimiser la valeur de la fonction objectif. Mais, il y a deux options: obtenir la valeur optimale supérieure (maximiser) ou d'obtenir la valeur optimale inférieure (minimiser).

Il y a également des différences dans l'algorithme entre l'objectif de maximisation et celui de la minimisation à propos du critère de condition d'arrêt pour terminer les itérations et les conditions d'entrée et de sortie de la base. Ainsi:

Objectif de maximisation
Condition d'arrêt: lorsque la ligne Z n'apparaît pas de valeur négative.

Condition d'entrée en base: la valeur la plus basse négative sur la ligne Z (ou la plus grande valeur absolue parmi les négatifs) indique la variable Pj entrante en base.

Condition de sortie de la base: après l'obtention de la variable entrante, la variable qui sort est déterminé par le quotient le plus faible de P0/Pj des strictement positifs.
Objectif de minimisation
Condition d'arrêt: lorsque sur la ligne Z il n'y a aucune valeur positive.

Condition d'entrée en base: la plus grande valeur positive sur la ligne Z indique la variable Pj qui rentre en base.

Condition de sortie de base: après l'obtention de la variable entrante, la variable qui sort est déterminé par le plus faible quotient de P0/Pj des strictement négatifs.

Cependant, il est possible de normaliser l'objectif du problème afin de toujours appliquer les mêmes critères par rapport à la condition d'arrêt de l'algorithme et les conditions d'entrée et sortie des variables de la base. De cette façon, si l'objectif est de minimiser la solution, on peut changer le problème à un autre équivalent de maximisation, simplement en multipliant la fonction objectif par "-1". Autrement dit, le problème de minimiser Z est équivalent au problème de maximisation (-1)·Z. Une fois la solution obtenue, il faudra aussi la multiplier par (-1).

Avantages: Pas besoin de s'inquiéter par des nouveaux critères d'arrêt, de condition d'entrée ou de sortie de base puisqu'ils ne changent pas.

Inconvénients: Dans le cas où la fonction a tous les coefficients de ses variables basiques positifs, et en plus les contraintes sont du type d'inégalité "≤", si on effectue le changement de ces coefficients ils restent négatifs en accomplissant la condition d'arrêt dans la première itération (conformément à la ligne de la valeur de la fonction objectif, toutes les valeurs sont positives ou zéro). Obtenant dans ce cas par défaut, une valeur optimale pour la fonction égale à zéro.

Solution: Ce problème n'existe pas vraiment, étant donné que pour que la solution soit supérieur à zéro, il est nécessaire qu'une contrainte ait imposé la condition " ≥" (et il serait un modèle pour la méthode des Deux Phases). Dans le cas en question, la vraie solution doit être zéro.

Inscrivez changement des termes indépendants

On dit aussi que les termes indépendants (bi) de chaque équation doivent être non négatifs afin d'utiliser la méthode du Simplexe. à cette fin, si certaines des contraintes présentent un terme indépendant plus bas que 0 il faudra la multiplier par "-1" (en tenant compte du fait que cette opération affecte également au type de contrainte).

Avantages: Avec cette simple modification de signes dans les contraintes correspondantes on facilite l'application de la méthode du Simplexe au problème de la modélisation.

Inconvénients: On peut trouver que dans les contraintes où on doit modifier les signes des constantes, les types d'inégalités sont "≤" (après l'opération, ils resteront du type "≥"), donc il sera nécessaire de développer la méthode des Deux Phases. Cet inconvénient n'est pas maîtrisable, mais autrement il pourrait se produire dans le cas contraire et d'être bénéfique si les termes indépendants sont négatives dans toutes les contraintes d'inégalité de type "≥". S'il y a des contraintes du type "=" ils n'entraînent pas des avantages ou désavantages car il serait toujours nécessaire d'appliquer la méthode des Deux Phases.

Normalisation des contraintes

Une autre condition du modèle standard du problème est que toutes les contraintes sont des équations d'égalité (autrement dites, contraintes d'égalité), il faudra changer les contraintes d'inégalité ou les inéquations en ces identités mathématiques.

La condition de non-négativité des variables (x1, ..., xn ≥ 0) est la seule exception et reste identique.

Contrainte de type "≤"
Pour normaliser une contrainte d'inégalité du type " ≤", on ajoute une nouvelle variable, appelée variable d'écart xs (sur la condition de non-négativité: xs ≥ 0). Cette nouvelle variable apparaît avec un coefficient zéro dans la fonction objectif, et en ajoutant dans l'équation correspondante (qui va maintenant être une identité mathématique ou une équation d'égalité).

a11·x1 + a12·x2 ≤ b1 a11·x1 + a12·x2 + 1·xs = b1
Contrainte de type "≥"
Dans le cas d'une inégalité de type "≥", on doit également ajouter une nouvelle variable appelée variable d'excès xs (avec la condition de non-négativité: xs ≥ 0). Cette nouvelle variable apparaît avec un coefficient zéro dans la fonction objectif, et en soustrayant l'équation correspondante.

Or, un problème se pose avec la condition de non-négativité de cette nouvelle variable du problème. Les inéquations contenant le type d'inégalité "≥" seraient:

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 - 1·xs = b1

Lors de la première itération de la méthode du Simplexe, les variables de base ne seront pas à la base et deviendront zéro. Dans ce cas, la nouvelle variable xs, après convertir à zéro x1 et x2, prendra la valeur -b1 et ne accomplira pas la condition de non-négativité. On doit ajouter un autre variable xr, appelée variable artificielle, qui apparaîtra aussi avec un coefficient zéro dans la fonction objectif et en ajoutant dans la contrainte correspondante. Comme suit:

a11·x1 + a12·x2 ≥ b1 a11·x1 + a12·x2 - 1·xs + 1·xr = b1
Contrainte de type "="
Contrairement à ce qu'on pourrait penser, pour les contraintes de type "=" (malgré d'être des identités) on a également besoin d'ajouter des variables artificielles xr. Comme dans le cas précédent, le coefficient sera zéro dans la fonction objectif et il ajoutera dans la contrainte correspondante.

a11·x1 + a12·x2 = b1 a11·x1 + a12·x2 + 1·xr = b1

Dans ce dernier cas, il est clair que les variables artificielles sont en violation des lois de l'algèbre, de sorte qu'il sera nécessaire d'assurer que ces variables artificielles ont une valeur de 0 dans la solution finale. Ceci est accompli par la méthode des Deux Phases et donc on devra toujours le faire chaque fois qu'on a ce genre de variables.

Le tableau suivant résume le type de variable qui apparaît dans l'équation normalisée et son signe selon les inégalités:

Forme d'inégalité	Forme de la nouvelle variable
≥	- excès + artificielle
=	+ artificielle
≤	+ écart

Développement de la méthode du Simplexe

Une fois le modèle standardisé, il peut être nécessaire d'appliquer la méthode du Simplexe ou la méthode des Deux Phases. Voir dans la figure la manière d'actuation pour atteindre la solution du problème modélisé.

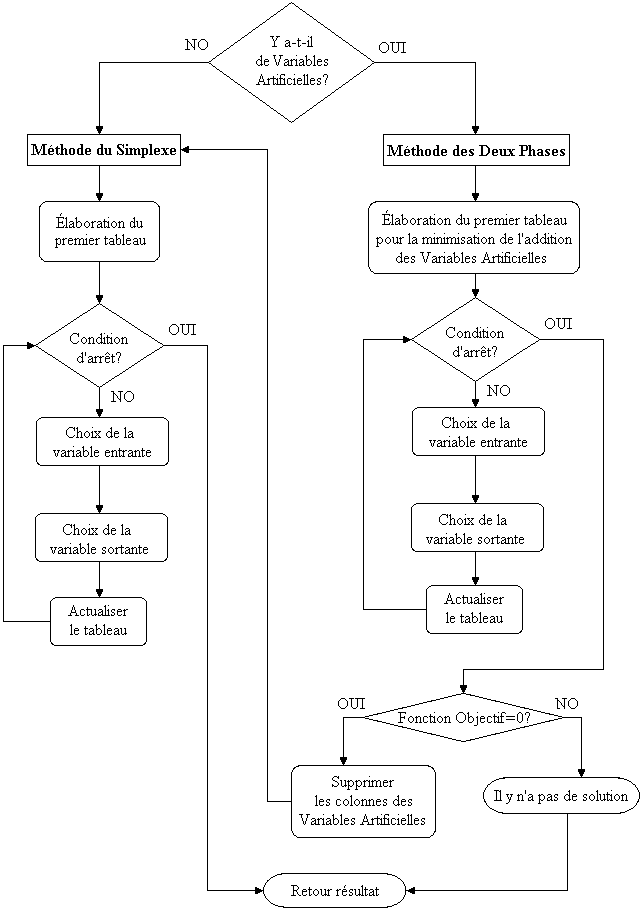
Les étapes de chaque méthode sont expliquées pas à pas ci-dessous, en précisant les aspects à prendre en considération.

Méthode du Simplexe

élaboration du premier tableau:

Les colonnes du tableau sont disposés comme suit: la première colonne du tableau contient les variables qui sont dans la base (ou variables basiques), c'est-à-dire, celles qui prennent la valeur pour offrir une solution, la deuxième colonne énumère les coefficients que ces variables de base ont dans la fonction objectif (cette colonne est appelé Cb), la troisième représente le terme indépendant de chaque contrainte (P0) ; à partir de cella, une colonne apparaît pour chacune des variables de décision et d'écart présentes dans la fonction objectif (Pj). Pour obtenir une vue plus claire du tableau, on ajoute une ligne qui contient les titres de chacune des colonnes.

Sur ce tableau, on ajoute deux nouvelles lignes: une d'elles, qui est à la tête du tableau, où les coefficients des variables de la fonction objectif se montrent, et une dernière ligne qui contient la valeur de la fonction objectif et les coûts réduits Zj - Cj.

Les coûts réduits montrent la possibilité d'une amélioration sur la solution Z0. C'est pourquoi sont aussi appelés des valeurs indicatrices.

Ce qui suit est l'aspect général du tableau de la méthode du Simplexe:

Tableau
			C1	C2	...	Cn
Base	Cb	P0	P1	P2	...	Pn
P1	Cb1	b1	a11	a12	...	a1n
P2	Cb2	b2	a21	a22	...	a2n
...	...	...	...	...	...	...
Pm	Cbm	bm	am1	am2	...	amn
Z		Z0	Z1-C1	Z2-C2	...	Zn-Cn

Toutes les valeurs du tableau sont fournies par le modèle du problème à moins que les valeurs de la ligne Z (ou ligne indicatrice). Elles sont obtenues comme suit: Zj = Σ(Cbi·Pj) pour i = 1..m, où si j = 0, P0 = bi et C0 = 0, autrement Pj = aij.

On observe, lors de l'exécution de la méthode du Simplexe, que dans ce premier tableau, toutes des variables d'écart occupent la base et donc (tous les coefficients des variables d'écart sont à 0 dans la fonction objectif) la valeur initiale de Z est nulle.

Pour la même raison, il n'est pas nécessaire d'effectuer les calculs de la réduction des coûts dans le premier tableau, et il peut être directement déterminée comme le changement de signe des coefficients de chaque variable dans la fonction objectif, -Cj.

Condition d'arrêt:
Il répond à la condition d'arrêt lorsque la ligne indicatrice ne contient pas de valeur négative parmi les coûts réduits (lorsque l'objectif est de maximiser), c'est-à-dire, qu'il n'y a aucune possibilité d'amélioration.

Si la condition d'arrêt n'est pas accomplie, il est nécessaire d'effectuer encore une itération de l'algorithme, c'est- à-dire, la détermination de la variable qui devient basique et cesse de l'être, de trouver l'élément pivot, de mettre à jour les valeurs du tableau et de vérifier si la condition d'arrêt s'accomplie cette fois.

Il est également possible de déterminer que le problème est restreint et sa solution pourra toujours être améliorée. Dans ce cas, il n'est pas nécessaire de poursuivre l'itération indéfiniment et on peut mettre fin à l'algorithme. Cette situation se produit lorsque dans la colonne de la variable entrante en base toutes les valeurs sont négatives ou nulles.
Choix de la variable qui entre en base:
Lorsqu'une variable devient basique, c'est-à-dire, elle entre en base, elle devient à faire partie de la solution. Notant la réduction des coûts dans la ligne Z, on décide que la variable de la colonne dans laquelle il s'agit de la valeur la plus faible (ou la valeur absolue la plus élevée) parmi les valeurs négatives entre en base.
Choix de la variable qui sort de base:
Une fois la variable entrante est déterminée, on détermine que la variable sortante de base est située dans la ligne dont le quotient P0/Pj est le plus petit des strictement positifs (étant donné que cette opération se fera uniquement lorsque Pj est supérieur à 0).
élément pivot:
L'élément pivot du tableau est marqué par l'intersection entre la colonne de la variable entrante et la ligne de la variable sortante.
Mise à jour du tableau:
Les lignes correspondantes à la fonction objectif et aux titres resteront inchangées dans le nouveau tableau. Toutes les autres valeurs faudra les calculer comme on l'expliqué ci-dessous:
- Dans la ligne d'élément pivot de chaque nouvel élément est calculée en tant que:
  Élément ligne pivot = Élément ancienne ligne pivot / Pivot
- Dans les lignes restantes chaque élément est calculé:
  Nouvel élément ligne = Élément ancienne ligne - (Élément ancienne ligne en colonne pivot * Nouvel élément ligne pivot)
De cette façon, on atteint que tous les éléments de la colonne de la variable entrante sont nuls sauf celui de la ligne de la variable sortante dont la valeur est 1. (Ceci est analogue à utiliser la méthode de Gauss-Jordan pour la résolution des systèmes d'équations linéaires).

Méthode des Deux Phases

La méthode des Deux Phases est utilisée lorsque les variables artificielles apparaissent sous forme standard ou canonique du problème. La première phase vise à résoudre le problème auxiliaire Z' afin de minimiser la somme des variables artificielles et de le rendre nul (dans le but d'éviter les incohérences mathématiques). Après avoir résolu le premier problème, et tant qu'il est comme prévu le résultat, le tableau qui en résulte est réorganisé pour une utilisation dans la deuxième phase sur le problème d'origine.

Sinon, le problème n'est pas faisable, c'est-à-dire, il n'y a pas de solution et il ne faudra pas continuer avec la deuxième phase.

PHASE 1

Cette première étape est analogue à la méthode du Simplexe, à exception de la construction de le premier tableau, en plus d'avoir besoin de tenir compte du résultat obtenu pour déterminer si la deuxième phase se développe.

Dans ce cas, le dernier tableau de cette phase sera, avec quelques modifications, utilisée en tant que tableau initiale pour la deuxième phase.

Construction du premier tableau:

On prépare de manière analogue à le tableau initiale de la méthode du Simplexe, mais avec quelques différences.

Comme indiqué, dans cette première phase on résout un problème auxiliaire (la minimisation de l'addition des variables artificielles) avec une fonction d'objectif auxiliaire. Par conséquent, dans la première ligne du tableau, qui montre les coefficients des variables de la fonction objectif, tous les termes, sauf les coefficients des variables artificielles, seront à zéro. La valeur de chacun de ces coefficients est "-1" car on minimise l'addition de ces variables (Ne pas oublier que minimiser Z 'est la même chose que maximiser (-1)·Z').

L'autre différence pour le premier tableau, c'est que maintenant, il est nécessaire de calculer la ligne Z (ou la ligne indicatrice).

Tableau
		C0	C1	C2	...	Cn-k	...	Cn
Base	Cb	P0	P1	P2	...	Pn-k	...	Pn
P1	Cb1	b1	a11	a12	...	a1n-k	...	a1n
P2	Cb2	b2	a21	a22	...	a2n-k	...	a2n
...	...	...	...	...	...	...	...	...
Pm	Cbm	bm	am1	am2	...	amn-k	...	amn
Z		Z0	Z1	Z2	...	Zn-k	...	Zn

Étant Zj = Σ(Cbi·Pj) - Cj pour i = 1..m, où si j = 0, P0 = bi et C0 = 0, et à l'inverse Pj = aij.

Condition d'arrêt et passage à la phase 2:
La condition d'arrêt est la même que dans la méthode du Simplexe. Autrement dit, lorsque dans la ligne indicatrice aucun des valeurs des coûts réduits est négatif (car, comme on a posé l'objectif est la maximisation de (-1)·Z ').

Accomplie la condition d'arrêt, il est nécessaire de déterminer s'il est possible de procéder à la deuxième phase afin d'obtenir une solution optimale du problème initial. Cela se fait en observant le résultat obtenu dans la première phase: si sa valeur est 0, cela signifie que le problème initial a une solution et il est possible de la calculer, dans le cas contraire, il indique qu'il n'est pas faisable et qu'il n'y a pas de solution.

PHASE 2

La deuxième phase de la méthode des Deux Phases est élaborée exactement comme la méthode du Simplexe, sauf qu'avant de commencer les itérations il faut supprimer les colonnes correspondantes aux variables artificielles, et reconstruire le tableau d'origine.

Supprimer colonne de variables artificielles:
Si nous sommes parvenus à la conclusion que le problème initial a une solution, on doit préparer notre tableau pour la deuxième phase. Cette étape est très simple, il suffit de supprimer les colonnes correspondantes aux variables artificielles.
Construction du tableau initiale:
Le tableau initial, dans ce cas, reste à peu près égal au dernier tableau de la première phase. La ligne de la fonction objectif devrait être modifié seulement par celle du problème initial et recalculer la ligne Z (de la même manière que dans le premier tableau de la phase 1).

À partir de ce point, toutes les itérations, jusqu'atteindre la solution optimale du problème, ne montrent aucune différence avec la méthode du Simplexe.

Identifier des anomalies et des solutions

Solution optimale: lorsque la condition d'arrêt est accomplie et il n'y a pas des variables artificielles en base avec une valeur positive (les valeurs sont indiquées dans la colonne P0), l'optimalité est atteinte. La valeur Z0 actuelle est la solution optimale du problème, elle est accomplie pour les variables qui sont en base. Si c'est un problème de minimisation, la valeur optimale obtenue est multipliée par "-1".

Solutions infinies: accomplie la condition d'arrêt, si une variable de décision non-base a une valeur 0 dans la ligne Z, veut dire qu'il y a une autre solution qui fournit la même valeur optimale pour la fonction objectif. Dans ce cas, le problème admit une infinité de solutions, toutes comprises dans le segment (ou une partie du plan, région de l'espace, etc., selon le nombre de variables du problème) défini par A·X1 + B·X2 = Z0. Grâce à une nouvelle itération et en faisant que la variable de décision ayant 0 dans la ligne Z entre en base, une solution différente est obtenue pour la même valeur optimale.

Solution illimité (restreinte): si toute la colonne de la variable entrante en base a tous les éléments négatifs ou nuls, il s'agit d'un problème restreint, c'est-à-dire, qu'il a une solution illimitée. Il n'y a aucune valeur optimale spécifique pour la fonction objectif, mais lorsque la valeur des variables augmente, la valeur Z augmente également sans violer les contraintes.

Il n'y a pas de solution: lorsqu'aucun point ne satisfait toutes les contraintes du problème, l'infaisabilité se produit n'ayant pas de solution possible pour cela. Dans ce cas, après avoir fini toutes les itérations de l'algorithme, il y a des variables artificielles en base dont la valeur est supérieure à zéro.

Même résultat variable entrante: quand il y a une égalité dans la condition de décision de variables entrantes on peut choisir l'une d'elles sans affecter la solution finale. Par contre, il y a une influence dans le nombre d'itérations nécessaires pour obtenir la solution. Il est conseillé d'opter pour les variables de base, car elles sont celles qui feront partie de la solution optimale.

Même résultat variable sortante: on peut de nouveau choisir l'une d'elles. Toutefois, afin de ne pas prolonger le problème et d'éviter l'entrée dans une boucle sans fin (cas dégénéré), on discrimine en faveur des variables de décision pour qu'elles restent dans la base. Dans le cas d'être dans la première phase de la méthode des Deux Phases, on optera pour sortir de base les variables artificielles.

Curiosité en Phase 1: à la fin de la phase 1, si le problème initial a une solution, toutes les variables artificielles dans la ligne indicatrice doivent être réglées sur " 1".

Peut être nul l'élément pivot? Non, l'élément pivot est toujours strictement positif puisqu'on n'effectue que les quotients parmi de valeurs non négatives et supérieures à zéro (face à un problème de maximisation).