PHPSimplex

Optimiser les ressources avec Optimisation Linéaire

Plus court chemin

Les problèmes connus comme problèmes de plus court chemin ou problèmes de cheminement, essayent de trouver le chemin plus court entre deux points. Cela peut s'agir de la distance entre les points d'origine et de destination ou bien le temps écoulé d'un point à l'autre. Il est très utilisé dans les problèmes des réseaux de communications.

Ce type de problèmes peut se résoudre moyennant la méthode du Simplexe, cependant, il y a d'autres méthodes plus efficaces comme l'algorithme de Dijkstra ou celui de Bellman-Ford.

Exemple

Une personne doit se déplacer tous les jours d'une ville A à une autre G. Elle analyse le trajet plus court avec la carte de routes. On montre les routes et les distances dans la prochaine figure:

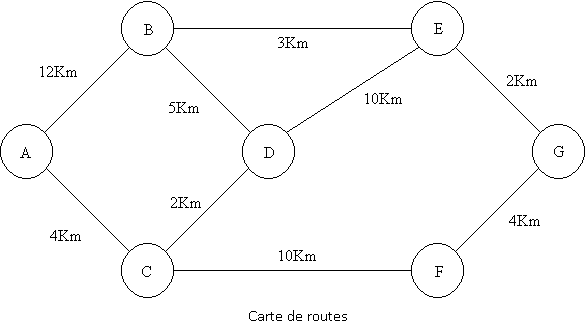
Déterminer les variables de décision et les représenter de manière algébrique. Dans ce cas:

Xij: fait de se déplacer de la ville i au j (0 il y a pas du déplacement, 1 il y a de déplacement)

Déterminer les contraintes et les formuler comme équation ou inéquations dépendants des variables de décision. Ces contraintes sont déduites du bilan entre les possibles trajets qui partent de chaque ville et ceux qui arrivent jusqu'à elle (en obviant à tous les trajets qui nous rendent au point de départ et ceux qui viennent du point de destination):

Bilan des trajets de la ville A: XAB + XAC = 1
Bilan des trajets de la ville B: XBD + XBE - XAB - XDB - XEB = 0
Bilan des trajets de la ville C: XCD + XCF - XAC - XDC - XFC = 0
Bilan des trajets de la ville D: XDB + XDC + XDE - XBD - XCD - XED = 0
Bilan des trajets de la ville E: XEB + XED + XEG - XBE - XDE = 0
Bilan des trajets de la ville F: XFC + XFG - XCF = 0
Bilan des trajets de la ville G: - XEG - XFG = -1

Présenter toutes les conditions implicitement établies conformément à la nature des variables: qu'elles ne peuvent pas être négatives, qu'elles soient entièrs, qu'elles ne peuvent que prendre valeurs déterminées, ... Dans ce cas les conditions sont que les variables doivent être booléens (0 on ne prend pas le chemin, 1 on prend le chemin), et par conséquent elles ne peuvent pas être négatives:

Xij ≥ 0
Xij sont booléens

Déterminer la fonction objectif:

Minimiser Z = 12·XAB + 4·XAC + 5·XBD + 3·XBE + 2·XCD + 10·XCF + 5·XDB + 2·XDC + 10·XDE + 3·XEB + 10·XED + 2·XEG + 10·XFC + 4·XFG

On effectue un changement dans la nomenclature des variables. La correspondance suivante s'établie:

XAB

XAC

XBE

XBD

XDB

XEB

XCD

XCF

XFC

XDC

XDE

XED

XEG

XFG

X10

X11

X12

X13

X14

Résoudre avec PHPSimplex.