PHPSimplex

Help: How to use the PHPSimplex tool

At the following lines, we will give a brief and simple guide about how to use the PHPSimplex tool. Once you had modeled the problem, that is, you have identified the objective function to maximize/minimize and its constraints, you can be sure that the hardest work is done.Let the PHPSimplex work for us.

Let's suppose that the modeled problem is the same that can be found in the section example of Simplex method, which have 2 basic or decision variables and 3 constraints. Then only have to indicate to the program, such data, like can be viewed in the screenshot.

Click the "Continue" button.

You must keep on providing data of the problem, in order for the algorithm be able to solve it. Facing the question, "Which is the objective of the function?", you should choose from the select if you want Maximize or Minimize, in the event that employs us you would take "Maximize". Fill in adequately the boxes of "Function" with the properly arguments for each decision variable, for this example it will be 3 and 2. Work at the same way to fill the constraints' boxes, taking special care with the inequality type for each one, because you can choose from select "≥", "≤" or "=".

PHPSimplex has an error control at the input user data, and checks if it is numbers. In the event that one or more box remain empty its value will be set to zero. Neither should worry about restricting the negative values of the decision variables, PHPSimplex will do it by itself. You should see something like its show in the following figure.

Now you can see the original problem as you typed it, and the problem into canonical form converted by PHPSimplex automatically.

At this point you can choose to view each iteration of the Simplex method (or Two Phases Simplex method) or not. PHPSimplex can display each table of the Simplex method (or Two Phases Simplex method) to help students, so if you are using PHPSimplex as an educational medium, you must click on the "Continue" button. However if you are making professional use of the tool, and just want to get the solution directly, bypassing all the intermediate steps, you must click on the option "Direct solution".

Clicking on "Continue" PHPSimplex will show you each iteration of the method that is being executed. The element which have green background colour, is the pivot element of the tableau.

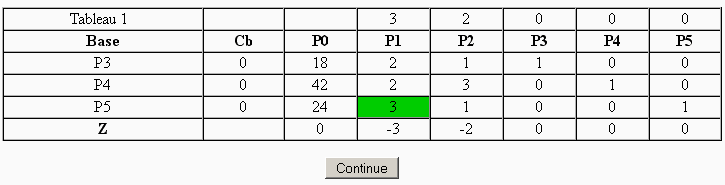
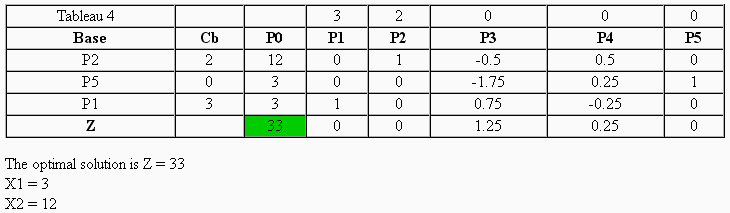
You only have to click on "Continue" to start a new iteration and generate the following tableau, until the method end. Once finished, PHPSimplex marks with green background colour the final result, and gives a little explanation of the solution obtained in both the case of existing or not, and why.

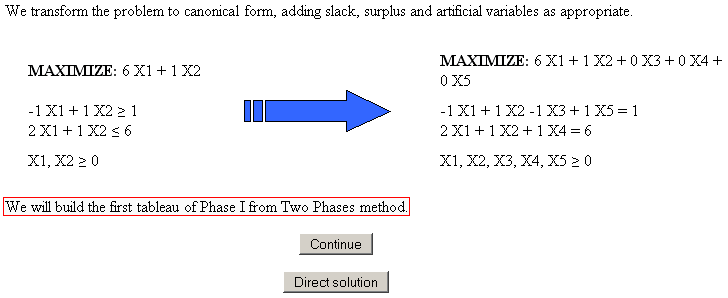
In order to finalize this guide for the tool, we will do mention to the case of that is accomplishing a problem and is necessary to do the Two Phase Simplex method. In the step of show the problem in standard form, PHPSimplex will notice you that you are going into Phase I of the Two Phase Simplex method.

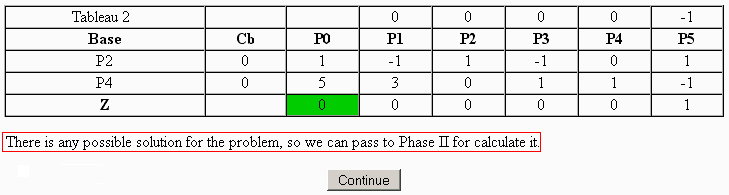
When the iterations are done, in the event that the original problem has solution, it is indicated that you will go to Phase II...

... or at the event that the problem has not solution, such information is given.

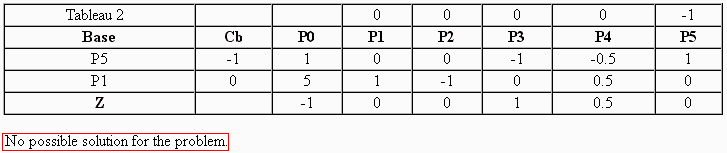
For the left iterations of the Two-Phase Simplex method, the way to execute is the same.