PHPSimplex
Optimizing resources with Linear Programming
Minimal road's problem
The problems known like minimal road's problem or shorter road problem, treat as its name shows to find the minimal or shorter route among two points. This minimum can be the distance among origin and destination points or else the elapsed time to go the route between that two points. It's usually used in communications networks problems.
This kind of problems can be solved by the Simplex Method, however exist another more efficient methods for example Dijkstra algorithm or other case can be Bellman-Ford algorithm.
Example
A person must go every day from village A to village G. He is studying with a roads map wich way is the shortest. The roads and its distances are shows in the following figure:
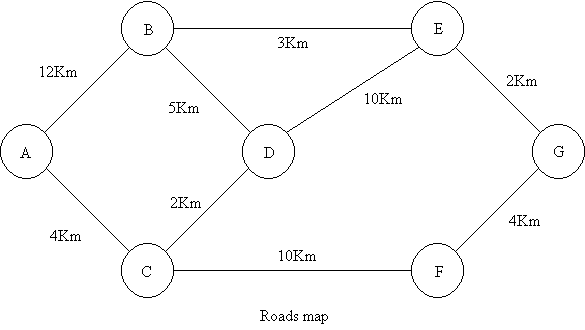
Determining decision variables and expressing them algebraically. In this case:
- Xij: action of moving from town i to j (0 indicates that there is no displacement and 1 that definitely there is displacement)
Determining the restrictions and expressing them as equations or inequalities in function of the decision variables. Such restrictions can be obteined from the balance among the possible ways that takes from each village and that wich arrive it (obviating the roads that take back to the starting point and the ones that come from the destination point):
- Roads' balance of village A: XAB + XAC = 1
- Roads' balance of village B: XBD + XBE - XAB - XDB - XEB = 0
- Roads' balance of village C: XCD + XCF - XAC - XDC - XFC = 0
- Roads' balance of village D: XDB + XDC + XDE - XBD - XCD - XED = 0
- Roads' balance of village E: XEB + XED + XEG - XBE - XDE = 0
- Roads' balance of village F: XFC + XFG - XCF = 0
- Roads' balance of village G: - XEG - XFG = -1
Expressing all implicit conditions established by the origin of variables: negativeness, integer, only a few allowed values... . In this case, the restrictions are that the variables must be boolean (0 the way isn't taken, 1 yes), and so, can't be negatives:
- Xij ≥ 0
- Xij are boolean
Determining objective function:
- Minimize Z = 12·XAB + 4·XAC + 5·XBD + 3·XBE + 2·XCD + 10·XCF + 5·XDB + 2·XDC + 10·XDE + 3·XEB + 10·XED + 2·XEG + 10·XFC + 4·XFG
Perform a change of variable with the following correspondence:
| XAB | XAC | XBE | XBD | XDB | XEB | XCD | XCF | XFC | XDC | XDE | XED | XEG | XFG |
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | X13 | X14 |